Convex uniform honeycomb

In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.

Twenty-eight such honeycombs exist:

the familiar cubic honeycomb and 7 truncations thereof;
the alternated cubic honeycomb and 4 truncations thereof;
10 prismatic forms based on the uniform plane tilings (11 if including the cubic honeycomb);
5 modifications of some of the above by elongation and/or gyration.

They can be considered the three-dimensional analogue to the uniform tilings of the plane.

1 History
- 1.1 Names
2 Compact Euclidean uniform tessellations (by their infinite Coxeter group families)
3 Noncompact forms
4 Hyperbolic forms
5 References
6 External links

History

1900: Thorold Gosset enumerated the list of semiregular convex polytopes with regular cells (Platonic solids) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions, including one regular cubic honeycomb, and two semiregular forms with tetrahedra and octahedra.
1905: Alfredo Andreini enumerated 25 of these tessellations.
1991: Norman Johnson's manuscript Uniform Polytopes identified the complete list of 28.
1994: Branko Grünbaum, in his paper Uniform tilings of 3-space, also independently enumerated all 28, after discovering errors in Andreini's publication. He found the 1905 paper, which listed 25, had 1 wrong, and 4 being missing. Grünbaum states in this paper that Norman Johnson deserves priority for achieving the same enumeration in 1991. He also mentions that I. Alexeyev of Russia had contacted him regarding a putative enumeration of these forms, but that Grünbaum was unable to verify this at the time.
2006: George Olshevsky, in his manuscript Uniform Panoploid Tetracombs, along with repeating the derived list of 11 convex uniform tilings, and 28 convex uniform honeycombs, expands a further derived list of 143 convex uniform tetracombs (Honeycombs of uniform polychorons in 4-space).

Only 14 of the convex uniform polyhedra appear in these patterns:

three of the five Platonic solids,
six of the thirteen Archimedean solids, and
five of the infinite family of prisms.

Names

This set can be called the regular and semiregular honeycombs. It has been called the Archimedean honeycombs by analogy with the convex uniform (non-regular) polyhedra, commonly called Archimedean solids. Recently Conway has suggested naming the set as the Architectonic tessellations and the dual honeycombs as the Catoptric tessellations.

The individual honeycombs are listed with names given to them by Norman Johnson. (Some of the terms used below are defined in Uniform polychoron#Geometric derivations.)

For cross-referencing, they are given with list indices from [A]ndreini (1-22), [W]illiams(1-2,9-19), [J]ohnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and [G]runbaum(1-28).

Compact Euclidean uniform tessellations (by their infinite Coxeter group families)

The fundamental infinite Coxeter groups for 3-space are:

The 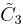${\tilde{C}}_3$ , [4,3,4], cubic, (8 unique forms plus one alternation)
The 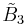${\tilde{B}}_3$ , [4,3^1,1], alternated cubic, (11 forms, 3 new)
The 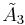${\tilde{A}}_3$ cyclic group, [(3,3,3,3)], (5 forms, one new)

In addition there are 5 special honeycombs which don't have pure reflectional symmetry and are constructed from reflectional forms with elongation and gyration operations.

The total unique honeycombs above are 18.

The prismatic stacks from infinite Coxeter groups for 3-space are:

The 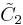${\tilde{C}}_2$ x ${\tilde{I}}_1$ , [4,4]x[∞] prismatic group, (2 new forms)
The 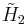${\tilde{H}}_2$ x ${\tilde{I}}_1$ , [6,3]x[∞] prismatic group, (7 unique forms)
The 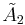${\tilde{A}}_2$ x ${\tilde{I}}_1$ , (3 3 3)x[∞] prismatic group, (No new forms)
The ${\tilde{I}}_1$ x ${\tilde{I}}_1$ x ${\tilde{I}}_1$ , [∞]x[∞]x[∞] prismatic group, (These all become a cubic honeycomb)

In addition there is one special elongated form of the triangular prismatic honeycomb.

The total unique prismatic honeycombs above (excluding the cubic counted previously) are 10.

Combining these counts, 18 and 10 gives us the total 28 uniform honeycombs.

The C^~₃, [4,3,4] group (cubic)

The regular cubic honeycomb, represented by Schläfli symbol {4,3,4}, offers seven unique derived uniform honeycombs via truncation operations. (One redundant form, the runcinated cubic honeycomb, is included for completeness though identical to the cubic honeycomb.)

Reference Indices	Honeycomb name Coxeter-Dynkin and Schläfli symbols	Cell counts/vertex and positions in cubic honeycomb
Reference Indices	Honeycomb name Coxeter-Dynkin and Schläfli symbols	(0)	(1)	(2)	(3)	Solids (Partial)	Frames (Perspective)	Vertex figure
J_11,15 A₁ W₁ G₂₂	cubic t₀{4,3,4}				(8) (4.4.4)			octahedron
J_12,32 A₁₅ W₁₄ G₇	rectified cubic t₁{4,3,4}	(2) (3.3.3.3)			(4) (3.4.3.4)			cuboid
J₁₃ A₁₄ W₁₅ G₈	truncated cubic t_0,1{4,3,4}	(1) (3.3.3.3)			(4) (3.8.8)			square pyramid
J₁₄ A₁₇ W₁₂ G₉	cantellated cubic t_0,2{4,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.4.4)			obilique triangular prism
J_11,15	runcinated cubic (same as regular cubic) t_0,3{4,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.4)	(1) (4.4.4)			octahedron
J₁₆ A₃ W₂ G₂₈	bitruncated cubic t_1,2{4,3,4}	(2) (4.6.6)			(2) (4.6.6)			(disphenoid tetrahedron)
J₁₇ A₁₈ W₁₃ G₂₅	cantitruncated cubic t_0,1,2{4,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.8)			irregular tetrahedron
J₁₈ A₁₉ W₁₉ G₂₀	runcitruncated cubic t_0,1,3{4,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.8)	(1) (3.8.8)			oblique trapezoidal pyramid
J₁₉ A₂₂ W₁₈ G₂₇	omnitruncated cubic t_0,1,2,3{4,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.8)	(1) (4.6.8)			irregular tetrahedron
J_21,31,51 A₂ W₉ G₁	alternated cubic h₀{4,3,4}	(6) (3.3.3.3)			(8) (3.3.3)			cuboctahedron

B^~₄, [4,3^1,1] group

The 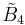${\tilde{B}}_4$ group offers 11 derived forms via truncation operations, four being unique uniform honeycombs.

The honeycombs from this group are called alternated cubic because the first form can be seen as a cubic honeycomb with alternate vertices removed, reducing cubic cells to tetrahedra and creating octahedron cells in the gaps.

Nodes are indexed left to right as 0,1,0',3 with 0' being below and interchangeable with 0. The alternate cubic names given are based on this ordering.

Referenced indices	Honeycomb name Coxeter-Dynkin diagram	Cells by location (and count around each vertex)				Solids (Partial)	Frames (Perspective)	vertex figure
Referenced indices	Honeycomb name Coxeter-Dynkin diagram	(0)	(1)	(0')	(3)	Solids (Partial)	Frames (Perspective)	vertex figure
J_21,31,51 A₂ W₉ G₁	alternated cubic			(6) (3.3.3.3)	(8) (3.3.3)			cuboctahedron
J_22,34 A₂₁ W₁₇ G₁₀	truncated alternated cubic	(1) (3.4.3.4)		(2) (4.6.6)	(2) (3.6.6)			rectangular pyramid
J_12,32 A₁₅ W₁₄ G₇	rectified cubic (rectified alternate cubic)	(2) (3.4.3.4)		(2) (3.4.3.4)	(2) (3.3.3.3)			cuboid
J_12,32 A₁₅ W₁₄ G₇	rectified cubic (cantellated alternate cubic)	(1) (3.3.3.3)		(1) (3.3.3.3)	(4) (3.4.3.4)			cuboid
J₁₆ A₃ W₂ G₂₈	bitruncated cubic (cantitruncated alternate cubic)	(1) (4.6.6)		(1) (4.6.6)	(2) (4.6.6)			isosceles tetrahedron
J₁₃ A₁₄ W₁₅ G₈	truncated cubic (bicantellated alternate cubic)	(2) (3.8.8)		(2) (3.8.8)	(1) (3.3.3.3)			square pyramid
J_11,15 A₁ W₁ G₂₂	cubic (trirectified alternate cubic)	(4) (4.4.4)		(4) (4.4.4)				octahedron
J₂₃ A₁₆ W₁₁ G₅	runcinated alternated cubic	(1) cube		(3) (3.4.4.4)	(1) (3.3.3)			tapered triangular prism
J₁₄ A₁₇ W₁₂ G₉	cantellated cubic (runcicantellated alternate cubic)	(1) (3.4.4.4)	(2) (4.4.4)	(1) (3.4.4.4)	(1) (3.4.3.4)			obilique triangular prism
J₂₄ A₂₀ W₁₆ G₂₁	cantitruncated alternated cubic (or runcitruncated alternate cubic)	(1) (3.8.8)		(2) (4.6.8)	(1) (3.6.6)			Irregular tetrahedron
J₁₇ A₁₈ W₁₃ G₂₅	cantitruncated cubic (omnitruncated alternated cubic)	(1) (4.6.8)	(1) (4.4.4)	(1) (4.6.8)	(1) (4.6.6)			irregular tetrahedron

A^~₃, [(3,3,3,3)] group

There are 5 forms^[1] constructed from the 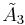${\tilde{A}}_3$ group, of which only the quarter cubic honeycomb is unique.

Referenced indices	Honeycomb name Coxeter-Dynkin diagram	Cells by location (and count around each vertex)				Solids (Partial)	Frames (Perspective)	vertex figure
Referenced indices	Honeycomb name Coxeter-Dynkin diagram	(0)	(1)	(2)	(3)	Solids (Partial)	Frames (Perspective)	vertex figure
J_21,31,51 A₂ W₉ G₁	alternated cubic		(4) (3.3.3)	(6) (3.3.3.3)	(4) (3.3.3)			cuboctahedron
J_12,32 A₁₅ W₁₄ G₇	rectified cubic	(2) (3.4.3.4)	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.3.3.3)			cuboid
J_25,33 A₁₃ W₁₀ G₆	quarter cubic	(1) (3.3.3)	(1) (3.3.3)	(3) (3.6.6)	(3) (3.6.6)			triangular antiprism
J_22,34 A₂₁ W₁₇ G₁₀	truncated alternated cubic	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.6.6)	(2) (4.6.6)			Rectangular pyramid
J₁₆ A₃ W₂ G₂₈	bitruncated cubic	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.6)			isosceles tetrahedron

Nonwythoffian forms (gyrated and elongated)

Three more uniform honeycombs are generated by breaking one or another of the above honeycombs where its faces form a continuous plane, then rotating alternate layers by 60 or 90 degrees (gyration) and/or inserting a layer of prisms (elongation).

The elongated and gyroelongated alternated cubic tilings have the same vertex figure, but are not alike. In the elongated form, each prism meets a tetrahedron at one triangular end and an octahedron at the other. In the gyroelongated form, prisms that meet tetrahedra at both ends alternate with prisms that meet octahedra at both ends.

The gyroelongated triangular prismatic tiling has the same vertex figure as one of the plain prismatic tilings; the two may be derived from the gyrated and plain triangular prismatic tilings, respectively, by inserting layers of cubes.

Referenced indices	symbol	Honeycomb name	cell types (# at each vertex)	vertex figure
J₅₂ A_2' G₂	h{4,3,4}:g	gyrated alternated cubic	tetrahedron (8) octahedron (6)	triangular orthobicupola
J₆₁ A_? G₃	h{4,3,4}:ge	gyroelongated alternated cubic	triangular prism (6) tetrahedron (4) octahedron (3)	-
J₆₂ A_? G₄	h{4,3,4}:e	elongated alternated cubic	triangular prism (6) tetrahedron (4) octahedron (3)
J₆₃ A_? G₁₂	{3,6}:g x {∞}	gyrated triangular prismatic	triangular prism (12)
J₆₄ A_? G₁₅	{3,6}:ge x {∞}	gyroelongated triangular prismatic	triangular prism (6) cube (4)

Prismatic stacks

Eleven prismatic tilings are obtained by stacking the eleven uniform plane tilings, shown below, in parallel layers. (One of these honeycombs is the cubic, shown above.) The vertex figure of each is an irregular bipyramid whose faces are isosceles triangles.

The C^~₂xI^~₁(∞), [4,4] x [∞], prismatic group

There's only 3 unique honeycombs from the square tiling, but all 6 tiling truncations are listed below for completeness, and tiling images are shown by colors corresponding to each form.

Indices	Coxeter-Dynkin and Schläfli symbols	Honeycomb name	Plane tiling
J_11,15 A₁ G₂₂	{4,4} x {∞}	Cubic (Square prismatic)	(4.4.4.4)
J₄₅ A₆ G₂₄	t_0,1{4,4} x {∞}	Truncated/Bitruncated square prismatic	(4.8.8)
J_11,15 A₁ G₂₂	t₁{4,4} x {∞}	Cubic (Rectified square prismatic)	(4.4.4.4)
J_11,15 A₁ G₂₂	t_0,2{4,4} x {∞}	Cubic (Cantellated square prismatic)	(4.4.4.4)
J₄₅ A₆ G₂₄	t_0,1,2{4,4} x {∞}	Truncated square prismatic (Omnitruncated square prismatic)	(4.8.8)
J₄₄ A₁₁ G₁₄	s{4,4} x {∞}	Snub square prismatic	(3.3.4.3.4)

The G^~₂xI^~₁(∞), [6,3] x [∞] prismatic group

Indices	Coxeter-Dynkin and Schläfli symbols	Honeycomb name	Plane tiling
J₄₂ A₅ G₂₆	t₀{6,3} x {∞}	Hexagonal prismatic	(6³)
J₄₆ A₇ G₁₉	t_0,1{6,3} x {∞}	Truncated hexagonal prismatic	(3.12.12)
J₄₃ A₈ G₁₈	t₁{6,3} x {∞}	Trihexagonal prismatic	(3.6.3.6)
J₄₂ A₅ G₂₆	t_1,2{6,3} x {∞}	Truncated triangular prismatic Hexagonal prismatic	(6.6.6)
J₄₁ A₄ G₁₁	t₂{6,3} x {∞}	Triangular prismatic	(3⁶)
J₄₇ A₉ G₁₆	t_0,2{6,3} x {∞}	Rhombi-trihexagonal prismatic	(3.4.6.4)
J₄₉ A₁₀ G₂₃	t_0,1,2{6,3} x {∞}	Omnitruncated trihexagonal prismatic	(4.6.12)
J₄₈ A₁₂ G₁₇	s{6,3} x {∞}	Snub trihexagonal prismatic	(3.3.3.3.6)
J₆₅ A_11' G₁₃	{3,6}:e x {∞}	elongated triangular prismatic	(3.3.3.4.4)

Examples

All 28 of these tessellations are found in crystal arrangements.

The alternated cubic honeycomb is of special importance since its vertices form a cubic close-packing of spheres. The space-filling truss of packed octahedra and tetrahedra was apparently first discovered by Alexander Graham Bell and independently re-discovered by Buckminster Fuller (who called it the octet truss and patented it in the 1940s). [2] [3] [4] [5]. Octet trusses are now among the most common types of truss used in construction.

Noncompact forms

Examples (partially drawn)
Cubic slab honeycomb	Alternated hexagonal slab honeycomb

If cells are allowed to be uniform tilings, more uniform honeycombs can be defined:

Families:

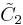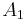${\tilde{C}}_2$ x $A_1$ : [4,4]x[ ] Cubic prismatic slab honeycomb (3 forms)
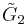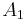${\tilde{G}}_2$ x $A_1$ : [6,3]x[ ] Tri-hexagonal prismatic slab honeycomb (8 forms)
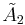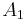${\tilde{A}}_2$ x $A_1$ : (3 3 3)x[ ] Triangular prismatic slab (No new forms)
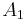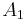${\tilde{I}}_1$ x $A_1$ x $A_1$ : [∞]x[ ]x[ ] = Cubic column honeycomb (1 form)
$I_2(p)$ x ${\tilde{I}}_1$ : [p]x[∞] Prismatic column honeycomb
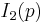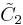${\tilde{C}}_2$ x ${\tilde{C}}_2$ x $A_1$ : [∞]x[∞]x[ ] = [4,4]x[ ] - = (Same as cubic slab honeycomb family)

Hyperbolic forms

Main article: Convex uniform honeycombs in hyperbolic space

There are 9 Coxeter group families of compact uniform honeycombs in hyperbolic 3-space, generated as Wythoff constructions, and represented by ring permutations of the Coxeter-Dynkin diagrams for each family.

From these 9 families, there are a total of 76 unique honeycombs generated:

[3,5,3] : - 9 forms
[5,3,4] : - 15 forms
[5,3,5] : - 9 forms
[5,3^1,1] : - 11 forms (7 overlap with [5,3,4] family, 4 are unique)
(4 3 3 3) : - 9 forms
(4 3 4 3) : - 6 forms
(5 3 3 3) : - 9 forms
(5 3 4 3) : - 9 forms
(5 3 5 3) : - 6 forms

The full list of hyperbolic uniform honeycombs has not been proven and an unknown number of non-Wythoffian exist. One known example is in the {3,5,3} family.

There are also 23 noncompact Coxeter groups of rank 4. These families can produce uniform honeycombs with unbounded facets or vertex figure, including ideal vertices at infinity:

Hyperbolic noncompact groups
7	, , , , , ,
7	, , ,, , ,
6	, , , , ,
3	, ,

References

^ [1], A000029 6-1 cases, skipping one with zero marks

John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
George Olshevsky, (2006, Uniform Panoploid Tetracombs, Manuscript (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
Branko Grünbaum, (1994) Uniform tilings of 3-space. Geombinatorics 4, 49 - 56.
Norman Johnson (1991) Uniform Polytopes, Manuscript
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Chapter 5: Polyhedra packing and space filling)
Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [6]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
A. Andreini, (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 75–129.
D. M. Y. Sommerville, (1930) An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, . 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes

External links

Weisstein, Eric W., "Honeycomb" from MathWorld.
Uniform Honeycombs in 3-Space VRML models
Elementary Honeycombs Vertex transitive space filling honeycombs with non-uniform cells.
Uniform partitions of 3-space, their relatives and embedding, 1999
The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
octet truss animation
Review: A. F. Wells, Three-dimensional nets and polyhedra, H. S. M. Coxeter (Source: Bull. Amer. Math. Soc. Volume 84, Number 3 (1978), 466-470.)
Richard Klitzing, 3D, Euclidean tesselations